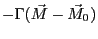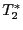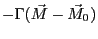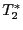ブロッホ方程式（ブロッホほうていしき、英: Bloch equations）とは、磁気共鳴の現象論的記述をする方程式を指す。1946年にフェリックス・ブロッホによって発表された。1957年に米国の物理学者リチャード・ファインマンはブロッホ方程式がより一般的な量子力学の2状態系における密度行列の時間発展の記述に適用できることを示し、アンモニアメーザーの解析に応用した。

概要

核スピンの集団があって、静磁場の中に置かれたとする。磁場の方向に z 軸を一致させた直交座標を選ぶ。核スピン全体の z 成分を Sz 、その熱平衡値を ⟨Sz⟩ と書く。核スピン全体の x 成分 Sx の熱平衡値は 0 である。 y 成分も同様である。核スピンは静磁場のまわりをラーモア歳差運動しているが、高周波に共鳴するとスピンの向きが逆転する。こうして熱平衡でなくなった核スピン集団は急速に熱平衡状態に戻ろうとする。静磁場を Hz、高周波の中の磁場成分を Hx , Hy とするとこの様子は

d S z d t = γ ( S x H y − S y H x ) − S z − ⟨ S z ⟩ T 1 d S x d t = γ ( S y H z − S z H y ) − S x T 2 d S y d t = γ ( S z H x − S x H z ) − S y T 2 {\displaystyle {\begin{aligned}{\frac {dS_{z}}{dt}}&=\gamma (S_{x}H_{y}-S_{y}H_{x})-{\frac {S_{z}-\langle S_{z}\rangle }{T_{1}}}\\{\frac {dS_{x}}{dt}}&=\gamma (S_{y}H_{z}-S_{z}H_{y})-{\frac {S_{x}}{T_{2}}}\\{\frac {dS_{y}}{dt}}&=\gamma (S_{z}H_{x}-S_{x}H_{z})-{\frac {S_{y}}{T_{2}}}\end{aligned}}}

で記述される。これらをブロッホ方程式という。γ は核磁気モーメント、T1 は縦緩和時間、T2 は横緩和時間である。

量子力学における2状態系

ブロッホ方程式は共鳴波長光に応答する原子の2準位系、光子の偏光状態、磁場に応答するスピン1/2の系等の一般的な量子力学における2状態系の記述に用いられる。

正規直交化された2状態を |1⟩, |2⟩ とすると、系の量子状態 |ψ(t)⟩ と密度行列 ˆρ は

| ψ ( t ) ⟩ = c 1 ( t ) | 1 ⟩ c 2 ( t ) | 2 ⟩ ( | c 1 ( t ) | 2 | c 2 ( t ) | 2 = 1 ) {\displaystyle |\psi (t)\rangle =c_{1}(t)|1\rangle c_{2}(t)|2\rangle \quad (|c_{1}(t)|^{2} |c_{2}(t)|^{2}=1)}
ρ ^ = | ψ ( t ) ⟩ ⟨ ψ ( t ) | = | c 1 | 2 | 1 ⟩ ⟨ 1 | c 1 c 2 ∗ | 1 ⟩ ⟨ 2 | c 2 c 1 ∗ | 2 ⟩ ⟨ 1 | | c 2 | 2 | 2 ⟩ ⟨ 2 | {\displaystyle {\hat {\rho }}=|\psi (t)\rangle \langle \psi (t)|=|c_{1}|^{2}|1\rangle \langle 1| c_{1}c_{2}^{\,\ast }|1\rangle \langle 2| c_{2}c_{1}^{\,\ast }|2\rangle \langle 1| |c_{2}|^{2}|2\rangle \langle 2|}

と表せる。このとき、恒等演算子とパウリ行列に対応する演算子

σ 0 ^ = | 1 ⟩ ⟨ 1 | | 2 ⟩ ⟨ 2 | = I ^ {\displaystyle {\hat {\sigma _{0}}}=|1\rangle \langle 1| |2\rangle \langle 2|={\hat {I}}}
σ 1 ^ = | 1 ⟩ ⟨ 2 | | 2 ⟩ ⟨ 1 | {\displaystyle {\hat {\sigma _{1}}}=|1\rangle \langle 2| |2\rangle \langle 1|}
σ 2 ^ = − i ( | 1 ⟩ ⟨ 2 | − | 2 ⟩ ⟨ 1 | ) {\displaystyle {\hat {\sigma _{2}}}=-i(|1\rangle \langle 2|-|2\rangle \langle 1|)}
σ 3 ^ = | 1 ⟩ ⟨ 1 | − | 2 ⟩ ⟨ 2 | {\displaystyle {\hat {\sigma _{3}}}=|1\rangle \langle 1|-|2\rangle \langle 2|}

を導入すると、密度行列は

ρ ^ = s 0 I ^ 2 s 1 σ ^ 1 2 s 2 σ ^ 2 2 s 3 σ ^ 3 2 {\displaystyle {\hat {\rho }}=s_{0}{\frac {\hat {I}}{2}} s_{1}{\frac {{\hat {\sigma }}_{1}}{2}} s_{2}{\frac {{\hat {\sigma }}_{2}}{2}} s_{3}{\frac {{\hat {\sigma }}_{3}}{2}}}

と展開できる。但し、展開係数は

s 0 = Tr ⁡ ( ρ ^ ) = | c 1 | 2 | c 2 | 2 = 1 {\displaystyle s_{0}=\operatorname {Tr} ({\hat {\rho }})=|c_{1}|^{2} |c_{2}|^{2}=1}
s 1 = Tr ⁡ ( σ ^ 1 ρ ^ ) = c 1 ∗ c 2 c 2 ∗ c 1 {\displaystyle s_{1}=\operatorname {Tr} ({\hat {\sigma }}_{1}{\hat {\rho }})=c_{1}^{\,\ast }c_{2} c_{2}^{\,\ast }c_{1}}
s 2 = Tr ⁡ ( σ ^ 2 ρ ^ ) = i ( c 1 c 2 ∗ − c 2 c 1 ∗ ) {\displaystyle s_{2}=\operatorname {Tr} ({\hat {\sigma }}_{2}{\hat {\rho }})=i(c_{1}c_{2}^{\,\ast }-c_{2}c_{1}^{\,\ast })}
s 3 = Tr ⁡ ( σ ^ 3 ρ ^ ) = | c 1 | 2 − | c 2 | 2 {\displaystyle s_{3}=\operatorname {Tr} ({\hat {\sigma }}_{3}{\hat {\rho }})=|c_{1}|^{2}-|c_{2}|^{2}}

で与えられる。ここで

s → ( t ) = s 1 e 1 → s 2 e 2 → s 2 e 3 → {\displaystyle {\vec {s}}(t)=s_{1}{\vec {e_{1}}} s_{2}{\vec {e_{2}}} s_{2}{\vec {e_{3}}}}

で定義される3次元単位ベクトルをブロッホベクトルといい、ブロッホベクトルがなす単位球面をブロッホ球という。

系のハミルトニアンを

H ^ = ℏ Ω 0 I ^ 2 ℏ Ω 1 σ ^ 1 2 ℏ Ω 2 σ ^ 2 2 ℏ Ω 3 σ ^ 3 2 = ℏ Ω 0 I ^ 2 ℏ Ω → ( t ) ⋅ σ → ( t ) 2 {\displaystyle {\hat {H}}=\hbar \Omega _{0}{\frac {\hat {I}}{2}} \hbar \Omega _{1}{\frac {{\hat {\sigma }}_{1}}{2}} \hbar \Omega _{2}{\frac {{\hat {\sigma }}_{2}}{2}} \hbar \Omega _{3}{\frac {{\hat {\sigma }}_{3}}{2}}=\hbar \Omega _{0}{\frac {\hat {I}}{2}} \hbar {\vec {\Omega }}(t)\cdot {\frac {{\vec {\sigma }}(t)}{2}}}

とすると、ブロッホベクトル s→(t) の時間発展は緩和項の無いブロッホ方程式

d d t s → ( t ) = Ω → ( t ) × s → ( t ) {\displaystyle {\frac {d}{dt}}{\vec {s}}(t)={\vec {\Omega }}(t)\times {\vec {s}}(t)}

で与えられる。こうした2状態系のブロッホ方程式による記述は、1957年にリチャード・ファインマンによって導入された。

脚注

参考文献

  • 『物理学辞典』 培風館、1984年
  • 北野正雄『量子力学の基礎』共立出版、2010年。ISBN 978-4320034624。 

関連項目

  • ブロッホ球

ブロッホ方程式 おにぎりまとめ

ブロッホ方程式

ブロッホ方程式

ブロッホ方程式 おにぎりまとめ

半導体物理学